首先恭喜你终于来到了最后的欧拉公式。废话少说,先看看他基本形式,请欣赏它的美:
$$ e^{ix} = cos(x)+i\sin(x) $$
或许你会问:这一堆符号,美在哪里呢?
首先这个公式包含我们高中学过的自然常数,三角函数,虚数单位 i。并且还结合成了一个等式。要知道这可是一个等式啊。什么意思呢?你可以用来做正变换和反变换。
而且这个公式还表明着一个有趣的几何图形。在复平面中的一个单位圆。(为什么呢?怎么发现的呢?)因为我们轻松的知道下面的公式。
$$ cos(x)^2 + sin(x)^2 = 1 $$
把 x 想象成角度,随着 x 的变化,点在单位圆上转圈圈。
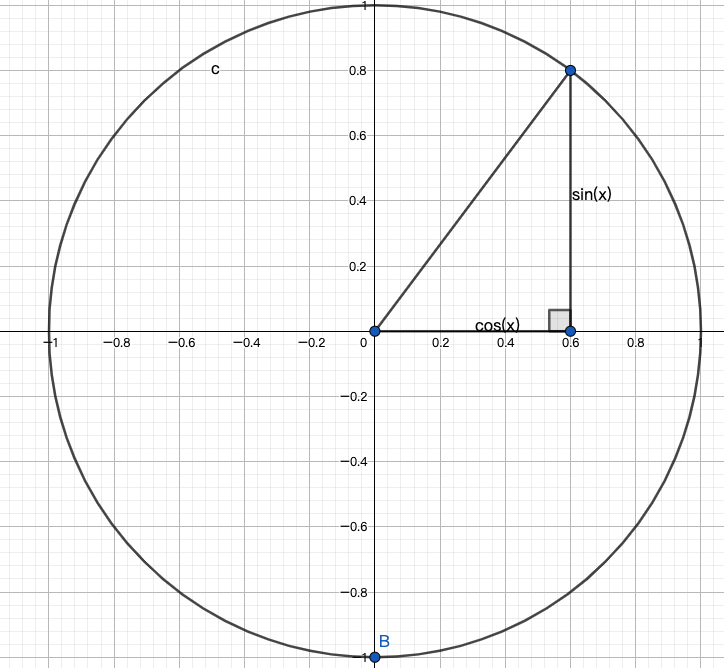
其中横坐标为复数的实部,纵坐标为实数的虚部。
那么欧拉公式是如何证明的呢?
在网络上或者一些书籍上尝试使用图像的证明方法。其中思路是证明e的ix次方,的图形确实是按照单位圆旋转的。其中包含很抽象和晦涩难懂的描述。这些证明和描述关于为啥:i表示一个向着逆时针的旋转,而e又是如何代表这连续。几乎使人听不懂,甚至更难理解。(我不知道读者之前关于那种论述的阅读体验如何,我理解能力有限,对于那么表现象的描述基本不理解。)
这里我将用纯代数的语言进行证明。我觉得这样才是最直观的。我的理解是先推出这个公式,再发现它是在单位圆上移动。
证明起来也非常的简单。总结起来就一句话。还是老东西了。x=ix带入到级数形式。然后分组。实部分一组,虚部分一组。最后逆用麦克劳林公式。(其实应该是三角级数)
$$ f(x) = f(0)+\frac{f'(0)}{1!}x + \frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+…+\frac{f^{(n)}(0)}{n!}x^n+o(x^n) $$
$$ sin(x) = x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+ … $$
$$ cos(x) = 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+ … $$
记忆的诀窍是sin是1,3,5,7而cos的是0,2,4,6,8.然后都是一正一负交替出现。当然如果你知道了原始的麦克劳林公式,可以重新推导。
由于虚数的平方为-1。很容易发现代入后可以得到上面的形式。为了辅助你思考。我们简单点来看看只有虚数单位的情况。
$$ \begin{array}{c|lcr} i次方数 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & ... \\ \hline 结果 & i & -1 & -i & 1 & i & -1 & - i & ... \end{array} $$
现在你可以发现后面也一样循环起来。如果只看计数都是虚部。而且正负交替。如果只看偶数,都是实部,也是正负交替。
于是你神奇的发现。在e的ix次方下竟然隐藏着正弦和余弦函数,而且只有使用虚数单位才能区分开了。
至此,这本书中关于自然常数项目的证明就全部结束了。是不是意犹未尽呢?数学就是这样,你会在探索中,寻找到其乐趣。而且你不需要什么电脑,也不需要什么高精度的实验设备。你只需要一支笔,一张纸,一本书,足以。
最后希望这部书的阅读过程可以使你快乐。谢谢。