0-1 分布
0-1 分布可以视为最简单的概率分布。一个随机事件只有两种可能 A 个非 A,于是我们两个离散的点 0,1 表示。其中比如 A 发生的概率是 p 那么非 A 发生的概率就是(1-p)。他的分布律如下
$$ P(X=k) = p^k .(1-p)^{1-k} $$
其中k=0,1在数学上使用 $X ~ B(x,p)$
这个很好理解,我们就拿抛一次硬币举例,要么证明正面朝上,要么反面朝上。
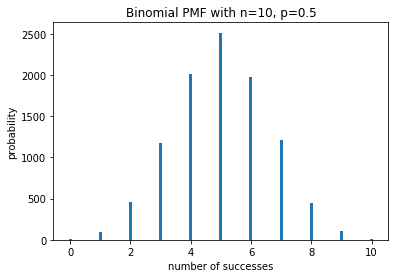
二项分布
好了现在我们要通过 0-1 分布过度到二项分布中来。
现在依旧以抛硬币这个事件来说。现在我们不是抛一次了,而是要实验 n 次(也就是人们说的 n 次独立伯努利试验)。现在我们要研究什么呢?不是出现正面的概率了,而想知道这 n 次实验之后出现正面次数 k 的概率。
为了方便研究我们先计算一个简单的情况:抛 3 次,正好出现 1 次的概率。这里抛了三次但是出现了一次正面,那么在哪次出现的正面呢?这出现的可能情况的个数显然是个组合数——$C_{3}^{1}$,这里表示在 3 个里面选择一个。
出现了一次正面的情况的个数乘以恰好出现一次的概率,应该就是其概率。如下:
$$ C_{3}^{1} p^{1} (1-p)^{3-1} $$
现在可以推广一下:把上面的实验次从 3 数变成 n,把出现的次数从 1 变成 k 我们就得到了二项分布的概率分布:
$$ P(X=k)=C^{k}_{n}p^k(1-p)^{n-k} $$
组合式计算公式:
$C_m^n = \frac{n!}{m!(n-m)!}$
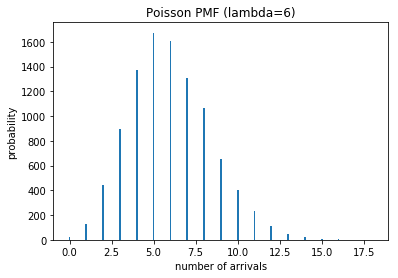
泊松分布
我们抛啊抛啊,抛了好久,但是却无法知道我们抛了一分钟的情况下出现正面的情况大约是多少。
现在泊松分布就要来解决这个问题了。我们要计算在单位时间内出现某个事件的概率来了。比如要计算出 10 分钟内某个医院中新生儿的个数。可是我们怎么计算呢?我们不能让每个母亲都去做实验看看她是生还是不生。我们有的数据仅仅是昨天一天来本医院的新生儿个数怎么办呢?
让我们看看有的数据是一种什么数据?是一种频率数据!就是在固定时间内的一种数学期望结果。如果假设一分钟前出生的个数对下一分钟没有什么必然的影响,他们在时间上相互独立的,也就是说我们得到的这个频率在统计上应该是稳定的。那么我们可否使用这个频率值进行估计呢?答案是可以的。怎么做呢?这里要用到极限的思想了。
首先我们承认在一段时间内发生的频率相对稳定我们叫它$\lambda$。注意这个一个合理的基本的假设。
现在我们把一段时间分成 n 等份,然后在每份时间里有做一次实验。
思考一下原来一段时间内发生的个数是 λ 现在分成了 n 份,也就是说在每一份中发生的概率为$p = \frac{\lambda}{n}$,于是不发生的概率为$1-p=1-\frac{\lambda}{n}$。
于是乎我们就有了一个 n 次独立伯努利实验。应用上一章节的公式得出:
$$ C^{k}_{n}p^k(1-p)^{n-k} $$
可是注意观察这里的 n 不是什么正经玩应儿!我们要的是和$\lambda$的关系啊。而且有些是就像生孩子这个事件一样我们可以近似为每时每刻都在实验中。相当于在一段时间内做了无数次的实验。好吧我们对 n 取极限吧!
$$ \lim*{n \to \infty,p \to 0} C^{k}*{n}p^k(1-p)^{n-k} $$
$$ \lim \frac{n(n-1)…(n-k+1)}{k!}p^k(1-p)^{n-k} $$
分子的每一项提取 n,于是总共提取了 k 个 n 相乘。
$$ \lim \frac{n^k[ 1(1-\frac{1}{n})…(1-\frac{k+1}{n})]}{k!}p^k(1-p)^{n-k} $$
因为 $n \to \infty$ 所以中括号里面的部分都变成了 1。于是乎原式为:
$$ \lim \frac{n^kp^k}{k!}(1-p)^{n-k} $$
现在看左边,由于我们知道$np = \lambda$;于是$\frac{n^kp^k}{k!} = \frac{\lambda^k}{k!}$
好了我们现在单单看看右侧的部分,先抄写一遍。
$$ \lim (1-p)^{n-k} $$
先简单的展开
$$ \lim(1-p)^n \lim (1-p)^k $$
可以知道$\lim (1-p)^k=1$,因为$p \ to 0$ 于是要考虑的就剩下了$ \lim(1-p)^n$项就可以了。
先我们知道了$n=\frac{\lambda}{p}$代入:
$$lim(1-p)^{\frac{\lambda}{p}} $$
$e = \lim\_{n \to \infty } (1+\frac{1}{n})^n$
这里利用一个小技巧就可以得到:
$$ [ \lim(1+(-p)^{\frac{1}{-p}} ]^{-\lambda} = e^{-\lambda} $$
把上面两个结果合并起来,现在我们的就得到了单位时间内发生次数的概率分布。
$$ P(X=k) = \frac{\lambda^k}{k!} e^{-\lambda} $$